「算数嫌い」が口ぐせだった子が笑顔で解くようになった、算数好きになる方法

1. 算数が嫌いな子は意外と多い

算数嫌いの子が増えている背景

集団塾では、あらかじめ決まったカリキュラムに沿って授業を進めますので、お子様が授業内容について行けているか否かにかかわらず、どんどん先に進んで行ってしまいます。

表面的な解き方の暗記に追われ、本来の理解が追いつかないまま進んでしまうことで、多くのお子様が算数に苦手意識を持ってしまうのです。最上位クラスから離れれば離れるほど、このような状態になってしまいがちです。

2. “算数嫌い”になる原因は？

要するに、聞かれても答えられないのに聞かれ続けるから、嫌になってしまうのです。それだけのことです。（さしたる理由がないのに嫌い、という場合は相性ですから、ここでは除きます。）

特に指摘したいのは、次の2点です。

(1) よく分からないうちに先に進められてしまう

算数は積み上げの科目と言われます。前の段階のことを十分に理解しているから今回のことを理解できるということです。

例えば、1箱3個入りのおまんじゅうが2箱あるとき、合わせて3×2で6個のおまんじゅうがあるということがわかると、1秒間に3m進むと2秒では3×2で6m進むことも自然とわかります。

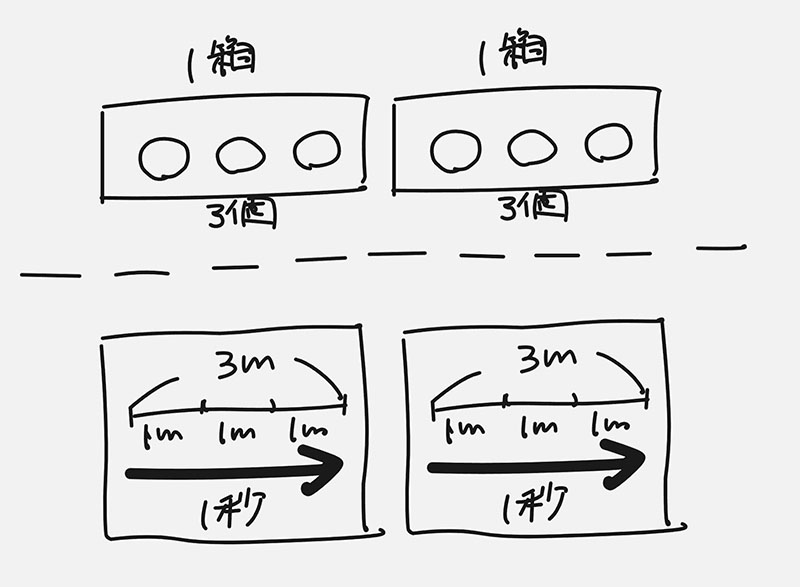
1箱3個入りの箱を、図解を通じて1秒間に3m進むことに読み替えれば、同じかけ算の式で表すことができるのは当然だということになります。

（1あたり量）×（個数）＝（合計）

（秒速）×（秒数）＝（進んだ長さ）　→　（速さ）×（時間）＝（道のり）

これらは同じようなことであるとわかれば、自然に別の単元に応用がききますし、結果として公式を覚えたのと同じような状態になります。

ということは、前の段階の内容がよく分からず、納得がいかない状態のまま新しいことを習っても、理解するための土台がないため分からないということになってしまいます。

これを繰り返して行くと、ますます分からないことが積み上がっていくだけの、いわば負のスパイラル状態に陥ります。当然、テストで得点は取れませんから、成績は上がらず・・・となっていくだけです。これでは、算数を好きになるはずがありません。

(2) 知識が「うろ覚え」状態にとどまっている

日常生活では、うろ覚えであっても「全く知らないよりはマシ」ということもあります。教養の一部となって役立つこともあるでしょう。しかし、試験の場では、試験では「うろ覚え」の知識は何の役にも立ちません。

「完璧に正確に覚えたものが」「短い時間で再現できる」

このようになって初めて、その知識は得点となってくれるのです。なんとなく解き方を知っているものをいくら増やしたところで、成績を上げるという目標を達成することはできません。できないものはできません。

3. 算数が好きになるための3つのステップ

では、どうするのか？どうすれば算数を好きになるのか？それは、通るべき道を一歩一歩進んでいくことにつきます。

以下、3つのステップを示します。（ステップ1だけでも十分に効果はございます。）

ステップ1：徹底的に基礎を固める

まずは、つまずいている問題、箇所、単元まで遡ります。小学校2年生で学習する内容から一つずつ丁寧に確認していくと、穴（つまずいている箇所）を的確に見つけることができます。

次に、扱う単元を決めたら、時間や効率を気にせず、正解を出せる状態を目指します。

• ・その単元に出てくる用語を理解し、再現できるようにする（図解も可）
• ・時間はいくらかかってもいいから、まずは正解できるようにする。
• ・何度でも、どれだけ期間がかかろうとも、できるようになるまでやる。

ここまで達成することが、徹底的に基礎を固めるということです。

要するに、この3つを行うということです。

• ・無理なくできる内容を扱う
• ・無理なくできる分量にとどめる
• ・身につくまで何度でも期間を問わず徹底的に繰り返す

私の塾ではこれしかしていません。

生徒が「わかってきた！」という実感を持つようになると、そう簡単に好きになるまではいかずとも、算数の問題に向かうことを嫌がらなくはなります。こうなれば、あとは辛抱強く見守りながら引き上げていくのみです。

ステップ2：文章題の解き方を知り、作業手順を身につける

単に解法の作業手順を覚えただけでは、その問題はできるけれど、見たことがない問題は解けないままです。

そこで、まずは解き方の手順を理解するところはゴールではなく、スタート地点であるという意識に切り替えてください。

その上で、詳しい解説があるテキストを使い、次のように進めます。
（市販のテキストでは、算数の予習シリーズをお薦めします。）

要するに、解き方（作業手順）を理解した上で覚えるということです。

解けて点数が取れないと嫌になってしまい兼ねませんので、まずは、得点できる状態を目指すことをお薦めします。

ただ、ここで終わると、扱った問題は解けるようになるものの、表現を変えられたりすると別の問題に見えるため、それは解けないということになります。あくまでも、解き方を覚えて解けるようになったことで、始めてスタート地点についただけであると認識しておくことが大切です。

そして、次の段階に進みます。

ステップ3：解き方と注目点を言語化し、再現できるようになる

前の段階で理解した作業手順を覚えるだけでは、解いたことがある問題はできるけれど、目先を変えた問題や見たことがない問題は解けないままにとどまります。

いわゆる応用がきくようにするために、解く作業ができるようになった解法について、その解法が成り立つ理由をつけていく作業に入ります。

とはいえ、その作業そのものは、前段階と同様にお手本を真似るだけです。
先ほどの詳しい解説があるテキストを使い、次のように進めます。（3）以外はステップ2の手順とほぼ同じです。

要するに、式を書く前に下記３つの作業を付け加えるのです。

• ・何に注目して解くかを書く
• ・読み取れたことを書く
• ・何の量を求めようとする式なのかを書く

これは、中学生以降では、記述式の答案といわれるものです。それを書くようにするのです。

記述式とはいいましても、自由作文ではありません。書き方には一定の型が存在します。それを手本を見ながら真似していくだけです。ある程度かけるようになるまでは、ひたすら真似れば十分です。

市販のテキストでは、算数の予習シリーズがいいお手本になります。例題の解説を手本として真似る（書き写す）のですが、そのときに式だけでなく、図や言葉も再現できるように取り組んでみてください。

試験範囲のほぼ全てがここまでできれば、偏差値が50を下回ることはございません。むしろ、概ね60を超えるのが当然という状態になります。（計算に弱点がある場合は、並行してその対策を行ってください。）

旅人算の問題を使った具体例

【問題】
A地点とB地点は600m離れています。甲はA地点から、乙はB地点からそれぞれ同時に出発し、甲はB地点に向かい、乙はA地点に向かいます。

甲、乙の進む速さがそれぞれ分速70m、分速50mであるとき、2人が出会うのは出発してから何分後ですか。そして、その場所はA地点から何mのところですか。

ステップ2(1)、ステップ3(1)：
まず、文章題の文章に書かれていることを図解する（内容を正しくつかむ）

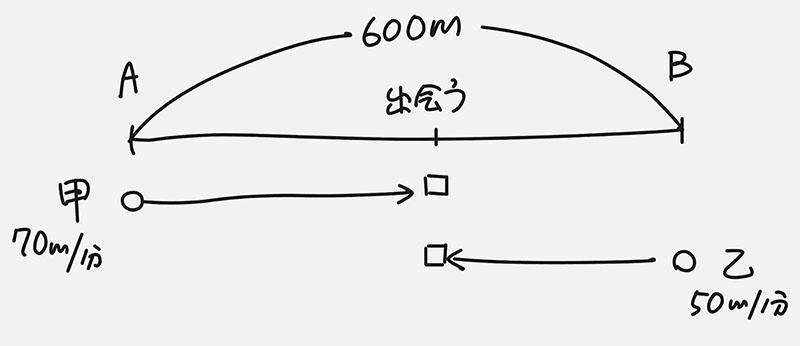
ステップ2(2)、ステップ3(2)：
単元ごとに読み取るべきポイント、注目すべき量を知り、図から読み取る

旅人算の問題では、注目すべき量は、「同じ時間に2人が進んだ道のりの和または差」であると事前に理解しておく。

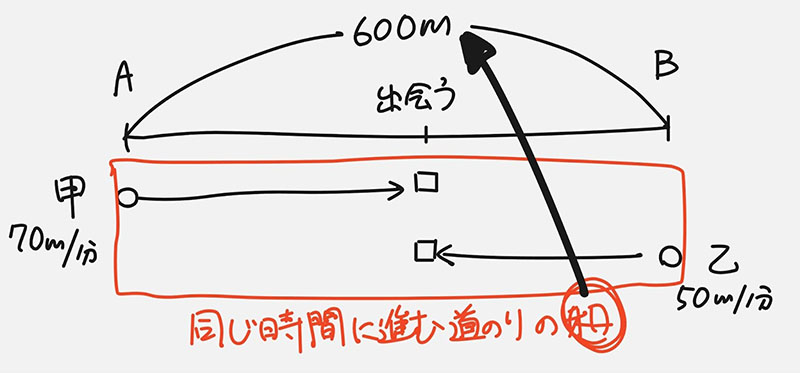
次からステップ2、ステップ3で変わってきます。

ステップ2(3) ：
読み取った内容をもとに、式を立てる（もちろん計算もする）

ステップ2(4) ：
そこで求めた値は何の量なのかを理解する

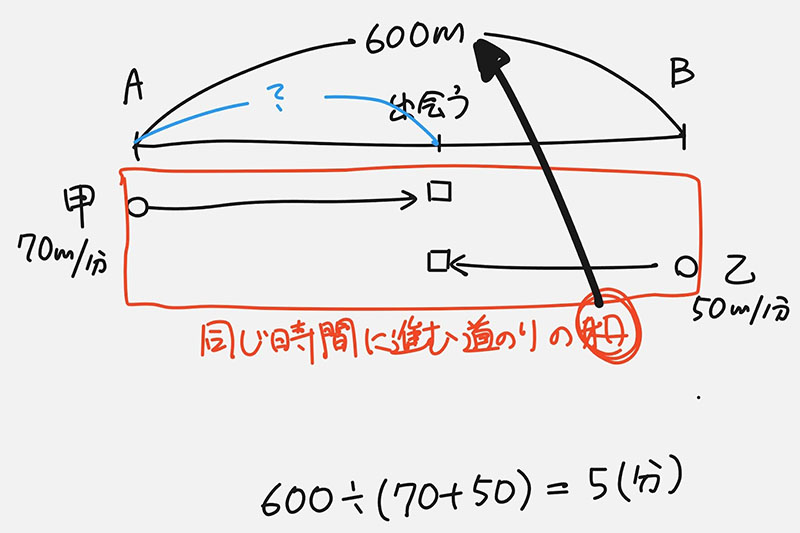
ステップ3(3)：
その読み取るべきポイント、注目した量、今回求めようとする量を言葉で書く！

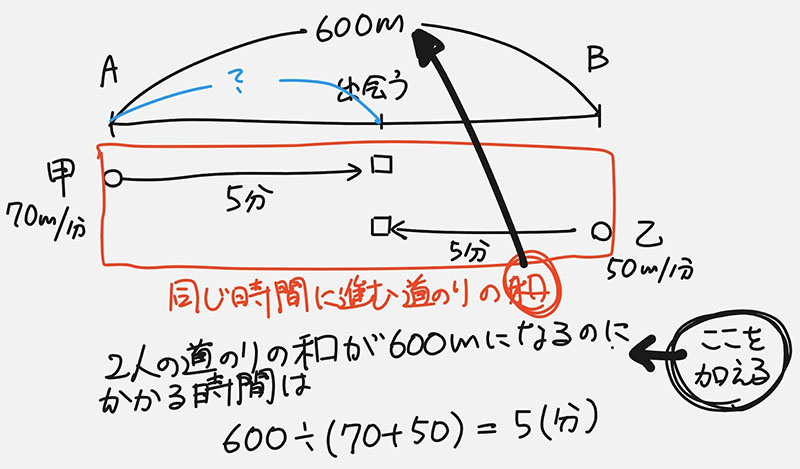
ステップ2(5)：必要に応じて(2)～(4)を繰り返し・・・

これは単に式を書いているだけ。

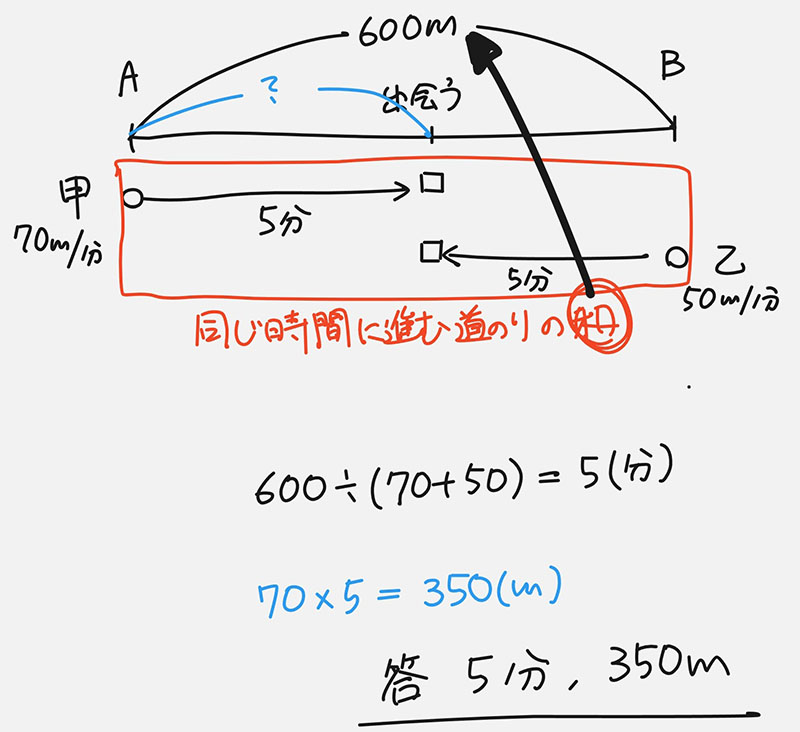
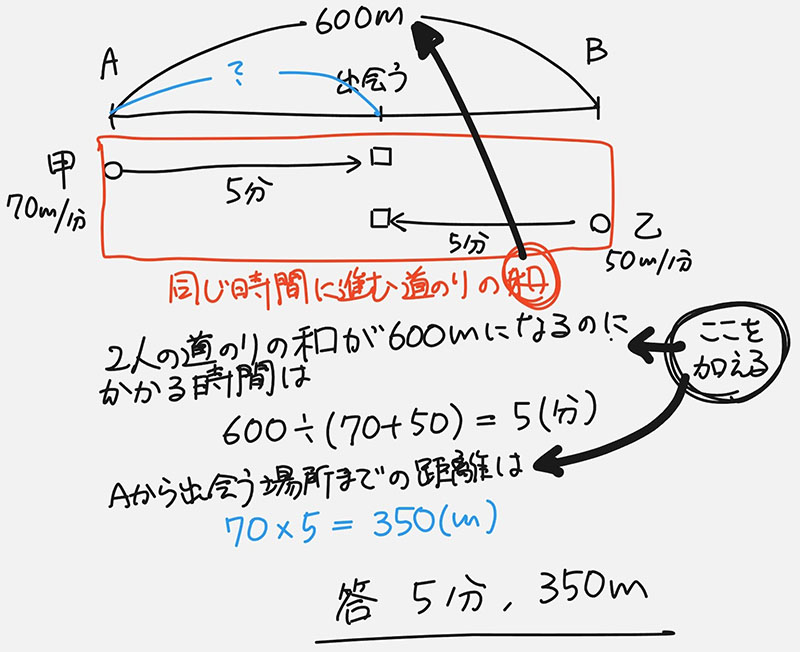
ステップ3(6) ：必要に応じて(2)～(5)を繰り返し・・・

これが記述式の答案（その式が表す量を式の前に書く）

4. 実際に算数嫌いだった子が変わった事例

まとめ

今回は以上です。

ご不明点やご質問、取り上げてほしい話題などがございましたらメッセージをお寄せください。次回以降に、必要に応じて適宜反映いたします。

個別のご相談も承りますので、ご入用の際は、お問い合わせください。お待ちしています。

執筆者プロフィール

神田算数・数学教室
東京都中央区（新富町駅・築地駅近く）
個別指導・オンライン指導対応
URL: https://kanda-math.net/

お子さまの算数・数学でお困りのことがございましたら、お気軽にご相談ください。