小6で出てくる“x”ってなに?意味がわかると算数がぐんと楽しくなる!
学校で使っている教科書では6年生で、 塾では早ければ 4年生頃に習うことになる文字ですが、実は小学校2年生の教科書に出てくる□や○などの記号と全く同じ意味合いのものです。よって、何も難しく考える必要はございません。
「 2に何を足したら5になるか?」というなぞなぞレベルのことを式で書くときに使う記号に過ぎないという程度のことです。

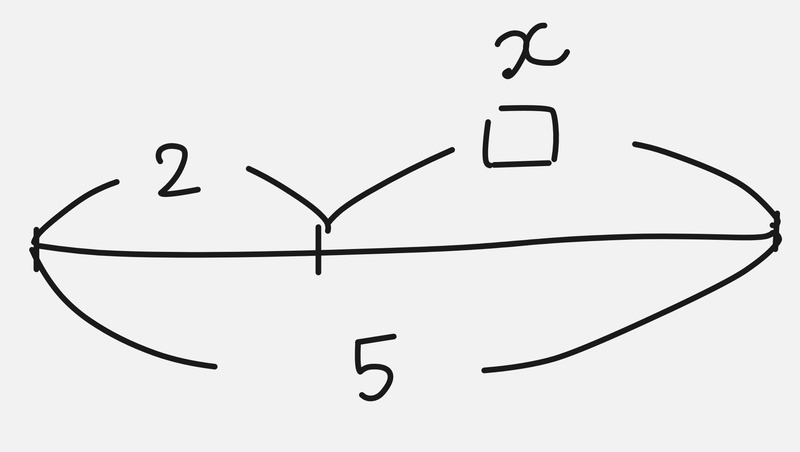
もちろん、式は \(2 + \square = 5 \) となりますが、これを次のように読み取る(解釈する)習慣をつけたいものです。
「2に何かを足すと5になるとき、その何かはいくつか?」
「□は、2にたすと5になるような数である。」
「2と□をたすと5になる。」
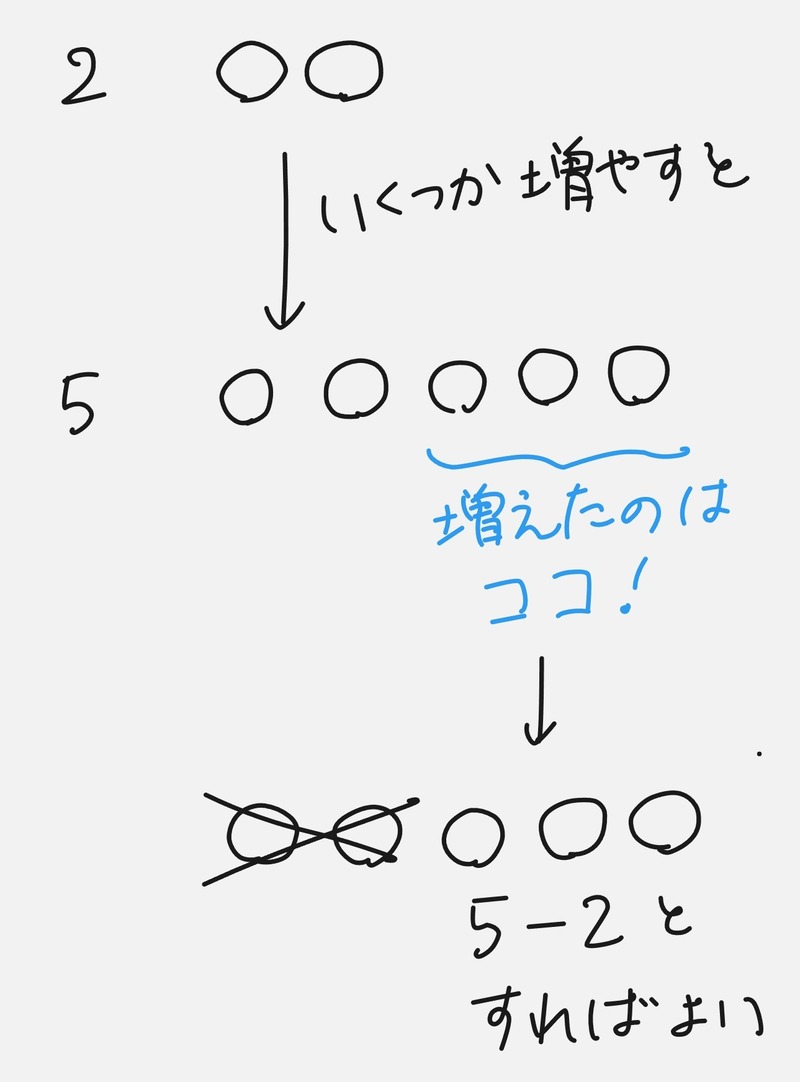
ここで、たし算は「2組のものを合わせて数える」「増やすことを表す」ときに使う計算であることを知っていれば、「2からいくら増やせば5になりるか?」と考えると、3とわかります。
図に表せば5-2という式を立てることにもつながります。すると、数が大きくなったり、分数や小数になって直感的に分からないときにも対応できるようになります。
式そのものは、□を求める問題であるととらえても良いし、単に2つの数をたしたら5になるということを表しているだけととらえてもよいということです。
“x”の正体は『変化する数』『まだ決まっていない数』
xなどの文字は、
・まだわかっていない数
・○の代わりに使う文字
・値がわからない数
・値は決まっているけれども隠されている数
・(代入するために)これから決める数
などいろいろな言い方はありますが、単なる数の代わりであると理解しておけば十分です。
補足しておきますと、下手に「xとは、わからない値のことである。」と表現を決めつけてしまうと、言語能力の高いお子さんですと、\(2+x=5\)という式を見たとき、「xは3と簡単にわかるので、『わからない値』とは言えないぞ」と考えこんでしまうこともあります。
xなどの文字は単に正体を明かされていない数に過ぎないということを理解してもらうよう配慮することをお薦めします。もちろん、当塾ではそうしています。
小6で突然出てくる“x”がわからない——よくあるつまずきとその解消法
とはいえ、□の入った計算になると間違いを連発する生徒をよく見かけます。原因は概ね3つに集約されます。
・見えている数や演算記号をなんとなく使って計算をしたがる
・実は四則演算の意味や計算規則をよくわかっていない
・理屈よりも計算のしやすさを優先する
一番目の「見えている数や演算記号をなんとなく使って計算をしたがる」とは、
\(2+\square=5\) であれば、見えている2と5と+の記号をただ並べて
\(\square=2+5=7\) としてしまうということです。
この例のように直感的に正解が(3と)わかる場合は間違えなかったとしても、
\(37+\square=63\) であればどうでしょうか?
ここからパッと \(\square=63-37\) と考えられるでしょうか。
37と63の和が100であることから「□は100だ!」としてしまいがちなのです。
これが、「見えている数や演算記号をなんとなく使って計算をしたがる」ということです。
37+63の方が繰り下がりのある63-37よりも計算しやすく感じるため、ついこちらに流されがちです。
解消法は、あたりまえすぎるのですが、正しい解き方を身につけることにつきます。
具体的には、次の通りです。
(1)四則演算の意味を理解する
(2)四則演算を図解して表す
(3)□を求める計算方法を理解する
もちろん、その上で考えなくても正しい式を立てられるように訓練して身につけます。
かけ算とたし算が混ざるような場合は、さらに、次のような対策も必要です。
(1)かけ算とわり算でつながった部分はひとかたまり(の数)であると受け止める
(2)□を大きくしていく(2+□をさらに大きな□に替えていく)
(3)xや□などの未知数以外の数が2個になった式の解き方を理解する
という手順で解く力を身につけるのです。
例題で理解する!“x”はこんなときに便利になる
例題 (消去算、連立方程式)
みかん1個の値段はりんご1個の値段よりも150円安く、みかん2個とりんご3個の値段の合計は950円です。りんご1個の値段を求めなさい。
解答
まず、みかんの方が安いので、それを線分図に表します。
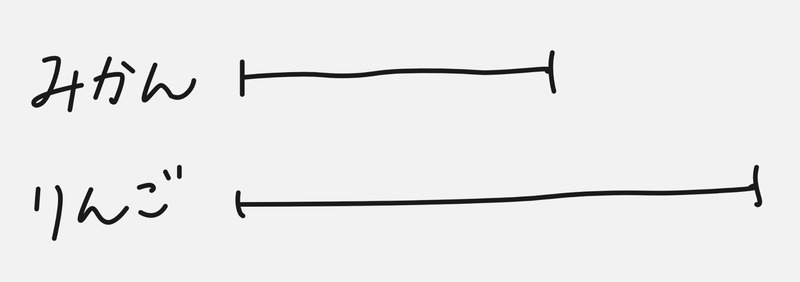
次に、150円の差をこの図に書き込みます。

求める値であるりんご1個の値段をx円とおき、図を見て式を立てます。
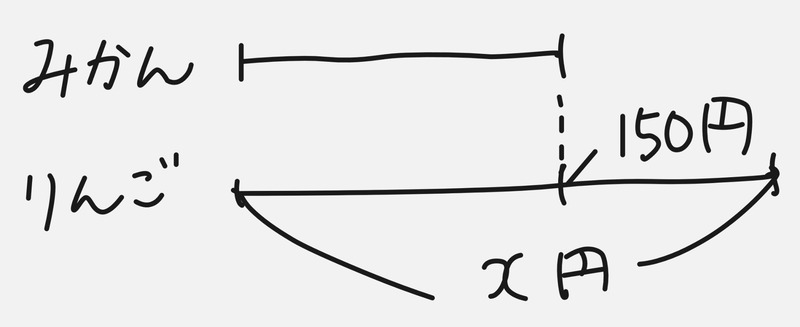
りんご1個の値段を\(x\)円とすると、みかん1個の値段は\((x-150)\)円となる。
ここで「みかん1個の値段はりんご1個の値段よりも150円安く」という情報は使い終わりましたから、次の「みかん2個とりんご3個の値段の合計は950円です」に注目します。
みかん1個の値段はx-150、りんご1個の値段はxですから
\(みかん\times 2+りんご\times 3=950\) という式を立てます。
みかんとりんごはx-150、xですから
\((x-150)\times 2+x\times 3=950\) とすればよいことになります。
あとはこれを解けば完成です。
\(x\times 2-150\times 2+x\times 3=950\)
\(x\times 5-300=950\)
\(x\times 5=950+300=1250\)
\(x=1250\div 5=250\)
\(答 250円\)
中学数学につながる“xの使い方”3つのポイント
□やxが入った計算問題を与えられたときは、上記のことに注意して練習していただければ十分です。
一歩進めて、自ら□やxを使った式を立てて解けるようになると、対応できる問題の範囲が大きく広がります。
ここが中学数学につながるポイントです。
重要なことは次の3点です。
・何をxとするかを明記する
・等しい量を見つけ出す意識を持つ
・式を立てやすい表現パターンを知っておく
このことについて、詳しくは別の投稿で解説いたします。
“x”でつまずく子はココで壁にぶつかっていることが多い
繰り返すことになりますが、xといっても算数で使う□(数の代わり)と同じ役割であり、見た目が違うだけのことです。
中学校では未知数を含む等式を方程式と名付けて扱いますが、解き方そのものは小学校時代と何ら変わりません。
私が見る限り、方程式が苦手という生徒さんは例外なく
・四則演算の意味を言語化できていない
・計算規則と計算のくふう(分配法則など)の習熟が不十分である
という状況です。
克服のヒント——“x”はこう教えるとスッと入る
この単元に限りませんが、こう教えたら一発で理解する、という魔法の表現は残念ながらございません。
しかし、すっと理解できる手順で説明をし練習をしてもらうことで、つまずかずに解き方を身につけることは可能です。
その方法は次の通りです。
・四則演算の意味を理解し、言語化しておく
・計算規則と典型的なくふうのしかたを身につける
・簡単な計算は暗算できるようにする
意外と見落としがちなことですが、ここは小学校の学習範囲なので、中学校の教科書には詳しい説明がありません。
したがって、ここの習熟が不十分であれば、まずはそこから対策することが大切です。方程式の問題だけ解いていてもなかなか成果は上がりません。
そして、計算の速度も大切です。
ゆっくり時間をかければ正確に計算できる、というだけでは不十分です。
ある程度の暗算力は必要です。
2桁どうしの数の筆算はしてもよいのですが、3桁以内のたし算、ひき算や、1桁の数をかけたり、1桁の数でわったりする計算程度は暗算でほぼ瞬時に(かかっても10秒以内に)求めたいものです。
まとめ
xの対処方法は次の通りです。今回のテーマに絞っていえば、以下のことをお薦めします。
・四則演算の意味を理解し、言語化、図解化できるようにする
・計算規則と典型的なくふうの仕方を身につける
・暗算力を鍛える
一言でまとめれば、基礎が大事であるという、いつもの結論に落ち着きます。
ひとつずつ、基礎となる技術を積み重ねていくことが成績アップにつながります。ぜひ取り入れてみてください。
無料面談を行い、必要に応じて体験授業を設定することも可能です。
ご不明点やご質問、取り上げてほしい話題などがございましたらメッセージをお寄せください。次回以降に、必要に応じて適宜反映いたします。
個別のご相談も承りますので、ご入用の際は、お問い合わせください。お待ちしています。
執筆者プロフィール

神田算数・数学教室 塾長 神田寛元
東京大学理科1類卒業。受験指導歴10年以上。「偏差値20足りなくても志望校合格」を実現する指導スタイルで、通っている塾から志望校変更を薦められた生徒を初志貫徹で合格に導く。
「問題の解き方を覚えること」ではなく「考え方を理解し説明できること」を重視した指導により、模試の合格判定に関係なく志望校合格を実現。特に算数・数学の思考プロセスの言語化指導を得意とし、根本的理解に基づく学力向上をサポートしている。
神田算数・数学教室
東京都中央区(新富町駅・築地駅近く)
個別指導・オンライン指導対応
URL: https://kanda-math.net/
お子さまの算数・数学でお困りのことがございましたら、お気軽にご相談ください。
